Does logic apply to nature as well?
Today, let’s dive into the world of bees and honey by answering a perplexing question.
Question: Why is the honeycomb made of hexagons?
If you do a quick search on ‘Honeycombs’, you will see that it follows a universal structure made out of hexagonal walls. Like our species, bees have been around for a really long time which gives them plenty of time to design a perfect honeycomb structure.
Imagine this. You are given a plot of land to build a hotel with rooms of the same size & shape. You are not given any materials plus you have a tight budget to begin with. Now, think of the goal required before proceeding to the next paragraph.
The goal is to minimize the amount of materials used to build the hotel.
In mathematical terms, the goal will be ” To minimise the perimeter given a fixed area”
Let’s narrow down to the few types of suitable shapes based on the requirements below.
#1: No spaces in between the rooms
#2: Walls with equal length
The shape that came to mind would be a ‘Regular Polygon’
However, not all regular polygons can be tessellated. Since all corners of a regular polygons are the same, we can observe that the common angle of the polygon have to be divisible by 360 degrees.
Hence, there are only 3 shapes that meet both requirements.

Next, we need to find out the shape with the smallest perimeter given a fixed area.
We use an area of 1 square unit for the steps below just for simplification.
The detailed calculations can be found at the bottom of this post.
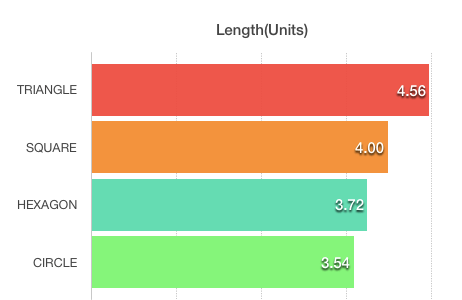
There you have it, the hexagon is the most efficient shape, proven by the language of science, also known as mathematics.
So bees are indeed brainy. Wish I could say the same about humans too.
Bonus: Did you notice a pattern above? Seems like the perimeter gets smaller when we increase the number of sides. If we just have to build a single room, can we use a regular polygon with infinite sides? I call it the infinite-gon, also known as the CIRCLE. Observe our surroundings. We can name plenty of objects that are circular for a reason, such as plastic bottles & aluminum cans.
Detailed Calculations
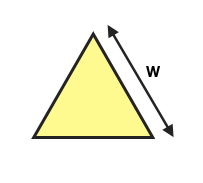
Area = ½ × w² × sin(60)
Perimeter = 3 × w
Since Area = 1,
w = √[2 × 1 ÷ sin(60)]
= 1.52 units
Hence,
P = 3 × 1.52 = 4.56 units
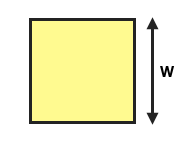
Area = w²
Perimeter = 4 × w
Since Area = 1,
w = √1
= 1 unit
Hence,
P = 4 × 1 = 4 units
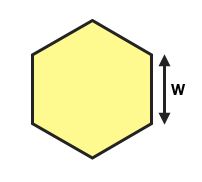
Note: A hexagon consists of six identical equilateral triangles
Area = 6[½ × w² × sin(60)]
Perimeter = 6 × w
Since Area = 1,
w = √[ 1 ÷ 3sin(60)]
= 0.62 units
Hence,
P = 6 × 0.62 = 3.72 units

Area = π × r²
Perimeter = 2 × π × r
Since Area = 1,
r = √[1 ÷ π]
= 0.564 units
Hence,
P = 2 × π × 0.564 = 3.54 units